The Spreadsheet NPV Function Actually Calculates Present Value, Not Present Value, As The Name Suggests. This revelation might surprise many spreadsheet users who rely on the NPV function for financial calculations. While the term "NPV" stands for Net Present Value, the function's mechanics deviate from the conventional understanding of net present value in financial analysis. This discrepancy arises from the way the function is programmed to interpret cash flows and discount rates. Understanding this subtle but significant distinction is crucial for accurate financial modeling and decision-making.
Spreadsheets are indispensable tools in finance, known for their ability to process complex calculations with ease. Yet, even the most seasoned financial analysts can sometimes misinterpret the functions these tools offer. The NPV function in spreadsheets is one such example where confusion can arise. It calculates the present value of future cash flows, but its name suggests otherwise. This misunderstanding can lead to miscalculations, impacting investment decisions and financial forecasting.
In this article, we will delve into the intricacies of the NPV function, clarifying its true purpose and examining how it operates within spreadsheets. We will explore the historical context of the function, its application in financial analysis, and provide step-by-step guidance on using it effectively. By the end, readers will gain a comprehensive understanding of why "The Spreadsheet NPV Function Actually Calculates Present Value, Not Present Value, As The Name Suggests" and how to apply this knowledge in real-world scenarios.
Table of Contents
- Understanding NPV: A Brief Overview
- Historical Context of NPV in Financial Analysis
- The Spreadsheet NPV Function: An In-Depth Look
- Common Misunderstandings and Their Implications
- Calculating Present Value with the NPV Function
- Real-World Applications of the NPV Function
- Step-by-Step Guide to Using the NPV Function
- Comparison with Other Spreadsheet Functions
- Impact on Financial Decision-Making
- Case Studies: Successes and Pitfalls
- Expert Tips for Accurate Financial Modeling
- Frequently Asked Questions
- Conclusion
Understanding NPV: A Brief Overview
The concept of Net Present Value (NPV) is a cornerstone of financial analysis, serving as a critical tool for evaluating the profitability of investments. At its core, NPV represents the difference between the present value of cash inflows and outflows over a specified period. It helps investors determine whether a project or investment will yield a return that exceeds its cost, taking into account the time value of money.
Time value of money is a fundamental financial principle that suggests a sum of money today is worth more than the same sum in the future due to its potential earning capacity. This principle is pivotal in NPV calculations, where future cash flows are discounted back to their present value using a chosen discount rate. The discount rate typically reflects the investor's required rate of return or the cost of capital.
In essence, a positive NPV indicates that the projected earnings, discounted for their present value, exceed the initial investment. Conversely, a negative NPV suggests that the investment's costs outweigh the returns, signaling a potential loss. This analysis aids investors and businesses in making informed decisions about where to allocate resources, prioritizing projects with the highest potential for value creation.
Historical Context of NPV in Financial Analysis
The roots of Net Present Value can be traced back to the early 20th century, when economists and financial theorists began to formalize methods for evaluating investment opportunities. The development of NPV as a financial metric was driven by the need for more sophisticated tools to assess the profitability of long-term projects, particularly in the context of industrial expansion and infrastructure development.
One of the earliest applications of NPV was in the field of corporate finance, where it was used to assess the viability of capital investment projects. As businesses sought to expand their operations, they needed reliable methods to evaluate which projects would deliver the greatest return on investment. NPV provided a framework for comparing different investment opportunities, allowing decision-makers to prioritize those with the highest potential for positive cash flows.
Over time, the use of NPV expanded beyond corporate finance to other areas, including real estate, energy, and public sector projects. Its adaptability and precision made it an essential tool for financial analysts and investment professionals. The widespread adoption of NPV was further facilitated by the advent of computer technology, which enabled more complex calculations and modeling, paving the way for its integration into modern spreadsheet software.
The Spreadsheet NPV Function: An In-Depth Look
The NPV function in spreadsheet software, such as Microsoft Excel and Google Sheets, is a powerful tool that simplifies the calculation of present value for a series of cash flows. However, its implementation differs from the traditional NPV calculation in financial analysis. This discrepancy has led to confusion among users, prompting a deeper examination of how the function operates.
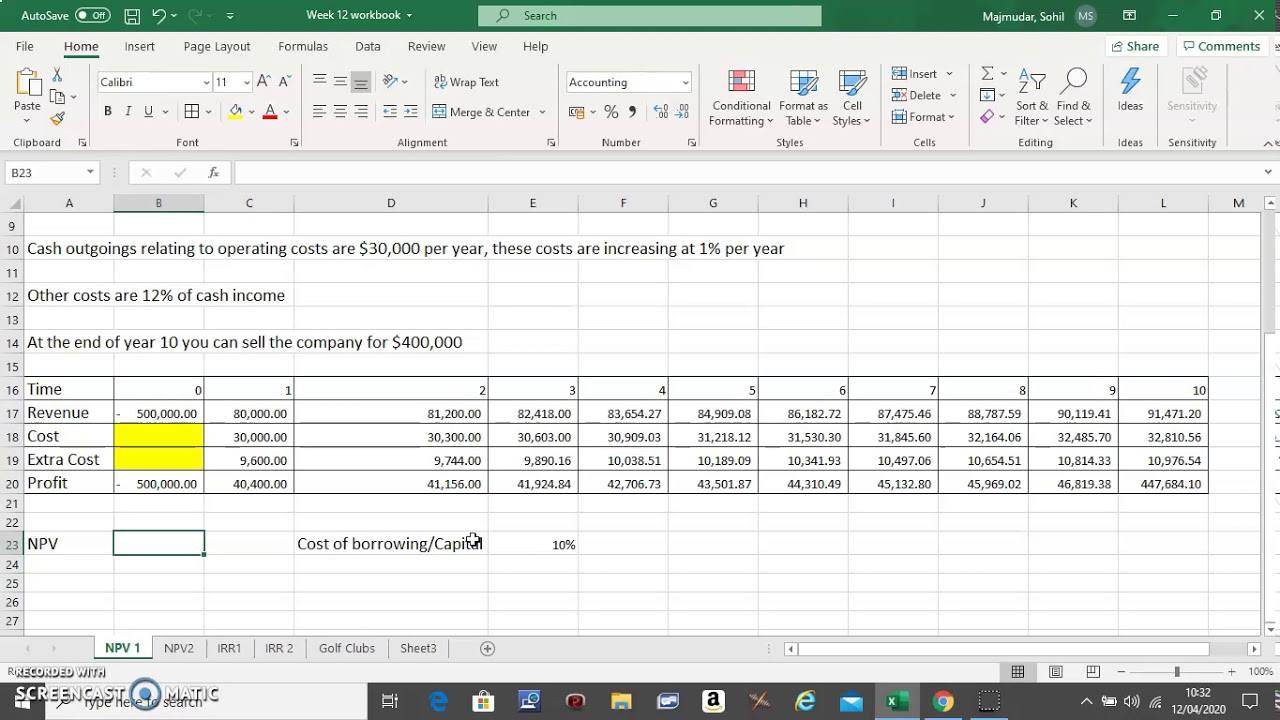
In spreadsheets, the NPV function calculates the present value of future cash flows based on a specified discount rate. Users input a series of cash flows, and the function returns the present value by discounting each cash flow to its present value and summing the results. This approach, however, differs from the traditional NPV calculation, which first subtracts the initial investment from the sum of discounted cash flows.
The distinction lies in the fact that the spreadsheet NPV function does not account for the initial investment, requiring users to manually adjust their calculations. This oversight can lead to inaccurate financial models if users assume that the function operates in the same manner as the traditional NPV formula. Consequently, it is essential for users to understand the nuances of the spreadsheet NPV function to ensure accurate financial analysis.
Common Misunderstandings and Their Implications
The primary misunderstanding surrounding the spreadsheet NPV function is the assumption that it calculates net present value in the same way as the traditional NPV formula. This misconception can lead to errors in financial models, as users may overlook the need to adjust for the initial investment.
Another common misconception is the belief that the NPV function accounts for cash flows occurring at different intervals. In reality, the function assumes that all cash flows occur at the end of each period, which may not align with the timing of cash flows in a given investment scenario. Users must take this into account when entering cash flows into the function, adjusting for any deviations in timing.
The implications of these misunderstandings can be significant, potentially leading to flawed investment decisions and inaccurate financial projections. For example, an investor relying on inaccurate NPV calculations may choose to pursue a project with a perceived positive NPV, only to discover that the project is unprofitable when the initial investment and timing of cash flows are properly accounted for.
Calculating Present Value with the NPV Function
To accurately calculate present value using the spreadsheet NPV function, users must first understand the mechanics of the function and how it differs from the traditional NPV formula. This involves recognizing that the function does not automatically deduct the initial investment from the calculated present value, requiring manual adjustments.
When using the NPV function, users should begin by entering the cash flows for each period into the spreadsheet. It is essential to ensure that these cash flows are aligned with the timing assumptions of the function, which assumes that all cash flows occur at the end of each period. Users must also specify a discount rate, which reflects the required rate of return or cost of capital for the investment.
Once the cash flows and discount rate are entered, the NPV function can be used to calculate the present value of the cash flows. However, to obtain the net present value, users must subtract the initial investment from the calculated present value. This step is crucial to ensure that the final result reflects the true profitability of the investment.
Real-World Applications of the NPV Function
The NPV function in spreadsheets is used in a variety of real-world applications, ranging from corporate finance to personal investment analysis. Its ability to simplify complex present value calculations makes it a valuable tool for decision-makers across industries.
In corporate finance, the NPV function is often used to evaluate capital investment projects, helping companies determine which projects will deliver the highest return on investment. By calculating the present value of projected cash flows, financial analysts can assess the profitability of different projects and prioritize those with the highest potential for value creation.
The function is also used in personal finance, where individuals can use it to evaluate investment opportunities, such as real estate or stock investments. By calculating the present value of future income streams, investors can assess whether an investment will generate a return that exceeds its cost, aiding in informed decision-making.
Step-by-Step Guide to Using the NPV Function
Using the spreadsheet NPV function effectively requires a clear understanding of its mechanics and how it differs from traditional NPV calculations. This step-by-step guide will help users navigate the process and ensure accurate financial modeling.
- Gather the necessary data: Before using the NPV function, gather all relevant cash flow data and determine the appropriate discount rate for the investment.
- Enter cash flows into the spreadsheet: Input the cash flows for each period into the spreadsheet, ensuring they align with the timing assumptions of the NPV function.
- Specify the discount rate: Enter the chosen discount rate, which reflects the required rate of return or cost of capital for the investment.
- Use the NPV function: Apply the NPV function to the cash flows and discount rate to calculate the present value of the cash flows.
- Adjust for the initial investment: Subtract the initial investment from the calculated present value to obtain the net present value.
- Interpret the results: Analyze the NPV result to determine the profitability of the investment. A positive NPV indicates a profitable investment, while a negative NPV suggests a potential loss.
Comparison with Other Spreadsheet Functions
While the NPV function is a valuable tool for calculating present value, it is not the only function available in spreadsheets for financial analysis. Other functions, such as the IRR and XNPV functions, offer alternative approaches to evaluating investment opportunities.
The IRR function calculates the internal rate of return, which represents the discount rate at which the net present value of cash flows is zero. This function is useful for comparing the profitability of different investments, as it provides a percentage return rather than a monetary value.
The XNPV function, on the other hand, accounts for cash flows occurring at irregular intervals, providing a more accurate calculation of present value in scenarios where cash flows do not occur at regular intervals. This function is particularly useful in industries where timing deviations are common, such as real estate or project finance.
By understanding the strengths and limitations of each function, users can choose the most appropriate tool for their specific financial analysis needs, ensuring accurate and reliable results.
Impact on Financial Decision-Making
The accurate calculation of present value is critical for informed financial decision-making, as it influences investment choices, capital allocation, and strategic planning. The spreadsheet NPV function, when used correctly, provides a reliable method for evaluating the profitability of investment opportunities.
However, misunderstandings surrounding the function's mechanics can lead to errors in financial models, potentially resulting in suboptimal investment decisions. By recognizing the nuances of the NPV function and adjusting for the initial investment and timing assumptions, decision-makers can ensure their analyses are accurate and reflective of true investment value.
The insights gained from accurate NPV calculations can inform a wide range of financial decisions, from project selection and resource allocation to risk management and performance evaluation. By leveraging the NPV function effectively, businesses and individuals can optimize their financial strategies and maximize value creation.
Case Studies: Successes and Pitfalls
Case studies offer valuable insights into the application of the NPV function in real-world scenarios, highlighting both successes and pitfalls. By examining these examples, users can gain a deeper understanding of the function's capabilities and limitations.
One notable success story involves a manufacturing company that used the NPV function to evaluate a proposed expansion project. By accurately calculating the present value of projected cash flows and adjusting for the initial investment, the company determined that the project would deliver a significant return on investment. This informed decision-making led to successful expansion and increased profitability.
Conversely, a common pitfall involves miscalculations due to misunderstandings of the NPV function. In one case, a real estate investor relied on inaccurate NPV calculations, failing to account for the initial investment and timing of cash flows. This oversight resulted in a poor investment decision, leading to financial losses.
These case studies underscore the importance of understanding the NPV function's mechanics and ensuring accurate calculations to avoid pitfalls and achieve successful outcomes.
Expert Tips for Accurate Financial Modeling
To ensure accurate financial modeling with the spreadsheet NPV function, experts offer several tips and best practices:
- Understand the function's mechanics: Familiarize yourself with the NPV function's assumptions and how it differs from traditional NPV calculations.
- Adjust for initial investment: Always subtract the initial investment from the calculated present value to obtain an accurate net present value.
- Account for timing: Ensure cash flows align with the function's timing assumptions, adjusting for any deviations in cash flow intervals.
- Use appropriate discount rates: Select a discount rate that accurately reflects the required rate of return or cost of capital for the investment.
- Cross-verify with other functions: Consider using alternative functions, such as IRR or XNPV, to validate results and gain additional insights.
By following these expert tips, users can enhance the accuracy and reliability of their financial models, leading to more informed and successful investment decisions.
Frequently Asked Questions
What is the main difference between the spreadsheet NPV function and traditional NPV calculations?
The main difference is that the spreadsheet NPV function does not automatically deduct the initial investment from the calculated present value, requiring users to manually adjust for this in their calculations.
Can the NPV function account for cash flows occurring at different intervals?
No, the NPV function assumes that all cash flows occur at the end of each period. Users must adjust for any deviations in timing when entering cash flows into the function.
What is the significance of the discount rate in NPV calculations?
The discount rate reflects the required rate of return or cost of capital for the investment, influencing the present value of future cash flows. Selecting an appropriate discount rate is crucial for accurate NPV calculations.
How can I ensure accurate financial modeling with the NPV function?
To ensure accurate financial modeling, understand the function's mechanics, adjust for the initial investment, account for timing, use appropriate discount rates, and cross-verify results with other functions.
What are some common pitfalls when using the NPV function?
Common pitfalls include failing to adjust for the initial investment, misunderstanding the timing assumptions, and using inappropriate discount rates, leading to inaccurate financial models.
Are there alternative functions to the NPV function in spreadsheets?
Yes, alternative functions include the IRR function, which calculates the internal rate of return, and the XNPV function, which accounts for cash flows occurring at irregular intervals.
Conclusion
The Spreadsheet NPV Function Actually Calculates Present Value, Not Present Value, As The Name Suggests. This nuanced understanding is vital for accurate financial analysis and decision-making. By recognizing the differences between the spreadsheet NPV function and traditional NPV calculations, users can avoid common pitfalls and ensure their financial models accurately reflect the true value of investments.
Through a comprehensive understanding of the NPV function's mechanics, careful selection of discount rates, and adjustment for initial investments and timing assumptions, users can leverage this powerful tool to make informed investment decisions. The insights gained from accurate NPV calculations can guide businesses and individuals in optimizing their financial strategies and maximizing value creation.
As the financial landscape continues to evolve, the NPV function remains a valuable asset for financial analysts and investment professionals. By mastering its application and understanding its limitations, users can harness its full potential and achieve successful outcomes in their financial endeavors.
Article Recommendations